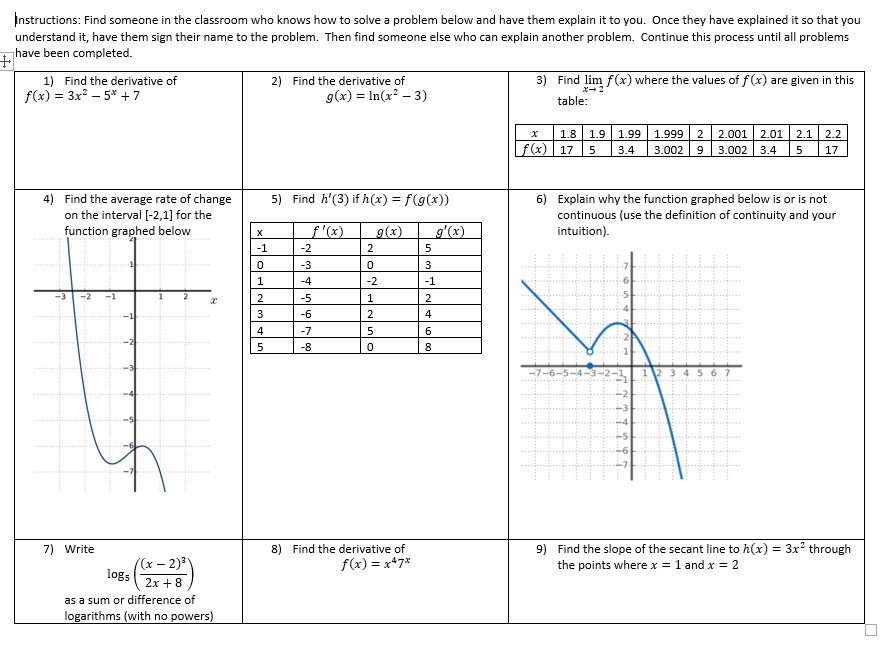
Escape room review sheet
For the review for test 1 in my Business Calculus course, I used the “Find Someone Who” activity featured in a previous post. When it was time to review for the second test, the students asked if we would be doing that again. Unfortunately, it didnt’ feel like a good fit with the content at that point in the class. So instead I concocted a low budget escape room. The pdf of my escape room is available here. If you want the .tex code you can acces it here, but I took out the QR code and link to my form, since you’ll need your own. If you want to try it our before you adapt it to your class, feel free to submit your answers to my Google Form (use the QR code in the pdf).
I got the idea for a digital escape room from a video I watched early in the pandemic. I learned the details of how to set one up using Google Forms from Bespoke ELA ‘s blog post. She explains the mechanics very well, so I won’t go into the details here. However, I will mention that the key step is to use “response validation” in the Google Form so that the students can’t go on unless they have entered the correct code.
For me the hardest part was thinking of a suitable story to frame the escape room and finding the right “voice”/writing style. In the end I chose to have the students need to find the manual over ride for the self-destruct sequence on our interstellar spaceship. I wrote in a campy style reminiscent ot the Choose Your Own Adventure books of my youth.
Here’s the introduction to my escape room:
We are the crew of the intergalactic spacecraft the USS Titan*. Captain Archey tripped and fell. On her way down, she hit her head on the self destruct button**. Now, she is unconscious and the 50 minute self-destruct count down has begun. Without the captain’s voice print, the only way to deactivate the self-destruct sequence is using the manual override switch.
The communications officer says, “I remember Captain Archey mentioning the instructions to deactivate it being on her e-reader.”
The exobiologist says, “I bet her e-reader is in her quarters. Does anyone know the passcode to enter her quarters?”
The head of security says, “She told me she left a hint to the code on a paper in her shoe whenever she had to change the code. Let’s hope she changed it recently.” The head of security removes Captain Archey’s shoe and finds the next page of this packet.
* Our university mascot is the Titans.
**I had three students at the front of the room to be the officers and read their parts. At this point in the story I flopped down on the floor and stayed down throughout the introduction.
All the “locks” in the escape room were codes to enter in the Google Form until the very end. After the students enter
ed the third code, which was the combination to my gym locker, they could head over to the front corner of the room where I had a laptop case/small carry on suitcase labled, “Captain Archey’s gym locker.”

Inside the “gym locker” they found a “key” (a picture of a key on cardstock) and a note indicating that the door to the manual shut off was in the back corner of the room.
In the back corner of the room there happened to be a little funny space between the wall and the window. Inside that space I put a switch controlling a red light (made of my kids’ Snap Circuits) and some cheap prizes like Lifesavers and pencils. To cover the space I had taped up a piece of paper with a door knob on it.

It was all kind of silly, but the students were good sports. One even asked me, “Are we really going to die if we don’t finish all these problems?”
I was actually walking around the room, but because in the story I was unconcious, the students made more of an effort to figure things out on their own (for example, digging through their notes rather than asking me for a formula).
Two of the three groups of students finished the activity and the third group was close. I was afraid that the students who didn’t finish might feel discouraged or disaapointed, but they actually came up to me after class and said what a great activity it was.